Linear Interpolation Formula: Step-by-Step Proof, Examples & Applications
Introduction
Linear interpolation is a mathematical method that is used to estimate any unknown value that falls between two known points. It solves points which are present in a straight line/linear relationship.
There are many different types of interpolation techniques used for solving complex and simple tasks alike, linear interpolation is the simplest of them and can be used in day-to-day tasks, you may be using it as well without even knowing it. Let’s dive into the topic.
History and Origins:
The concept of Linear Interpolation goes back to the early mathematics when people used it for navigation, this shows the importance of this technique and how it has been used since ancient times.
How Linear Interpolation Works
Basic Formula
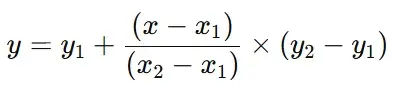
Here:
- x1, y1 and x2, y2 are the known points.
- x is the known value where interpolation is required
- y is the unknown value which is required.
You can use this formula to find any value along a straight line, Alternatively, you can use our easy-to-use calculator. The calculator also works on the same principle and you can get quick results in a few seconds, no need to perform manual calculations.
Applications:
Engineering:
Interpolation is widely used in engineering, from calculating properties like pressure, and temperature to finding stresses in a material.
Computer Animations:
It is used to create smooth transitions in animations and rendering visuals as well.
Data Estimation:
In between discrete data sets, unknown information can be interpolated which is essential in data estimation.
Advantages and Limitations:
| Advantages | Limitations |
|---|---|
| Easy to use | Only applicable to data that changes at a constant rate. |
| Computationally less resource-demanding | Errors may occur in data which is non-linear. |
| Efficient for small datasets | |
| Provides a unique solution for a given value. |
Example 1:
A temperature is known at 2 PM to be 20°C and at 4 PM to be 24°C. What will the temperature be at 3 PM?
Solution:
Here T1 and T2 are temperatures at time t1 and t2
t1 = 2, T1 = 20°C
t2 = 4, T2 = 24°C
t = 3
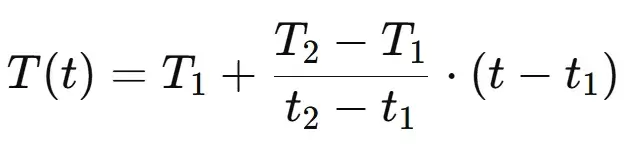
Substitute these values in the formula to get:
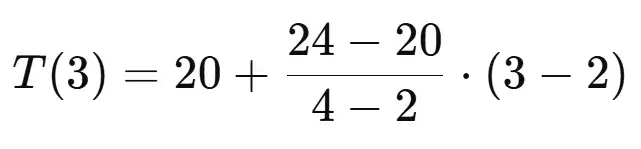
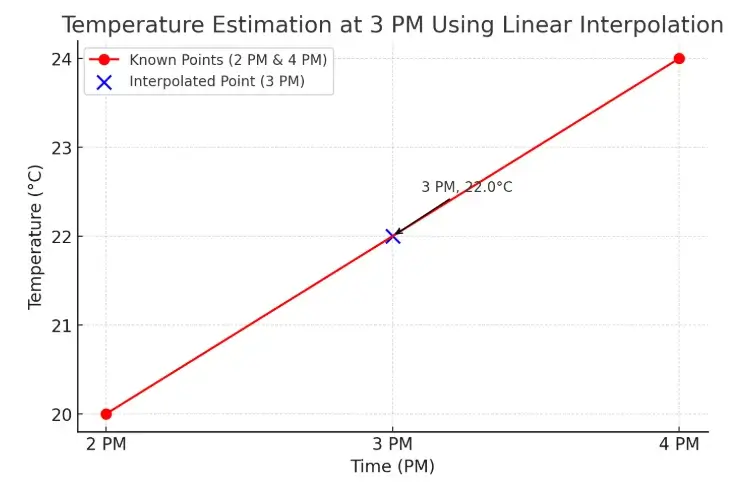
Solving for T(3)= 22°C.
The temperature at 3 PM is 22°C.
Example 2:
A child was 110 cm tall at age 6 and 130 cm at age 10. Estimate the height at age 8.
Solution:
t1 = 6, H1 = 110 cm
t2 = 10, H2 = 130 cm
t= 8
Using the formula:
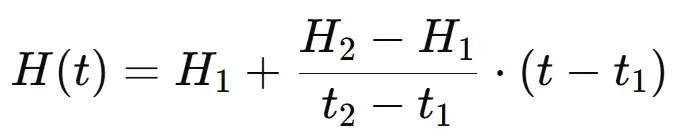
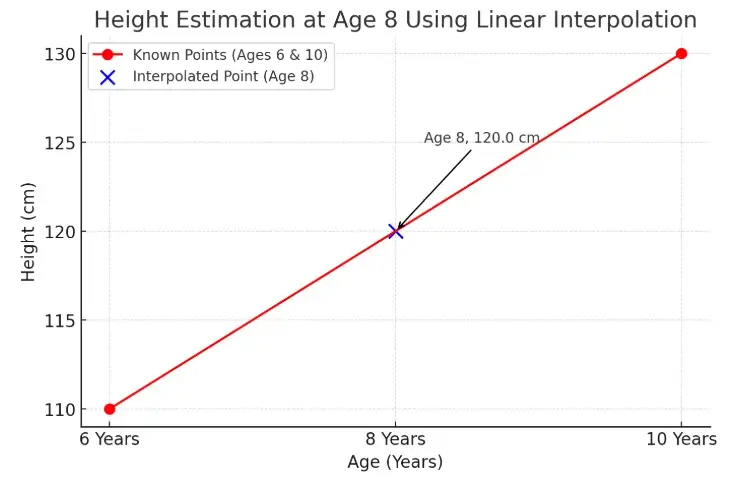
Substituting the values into the formula:
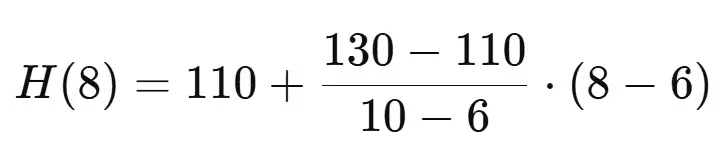
H(8) = 120 cm
Estimated height at age 8 will be 120cm.
Differences between Linear Interpolation and other methods:
Linear vs Cubic Spline Interpolation:
Cubic Spline interpolation has the advantage that it can work with non-linear data, it joins the data points with a smooth curve and it is more accurate as well, however, it requires more complex calculations.
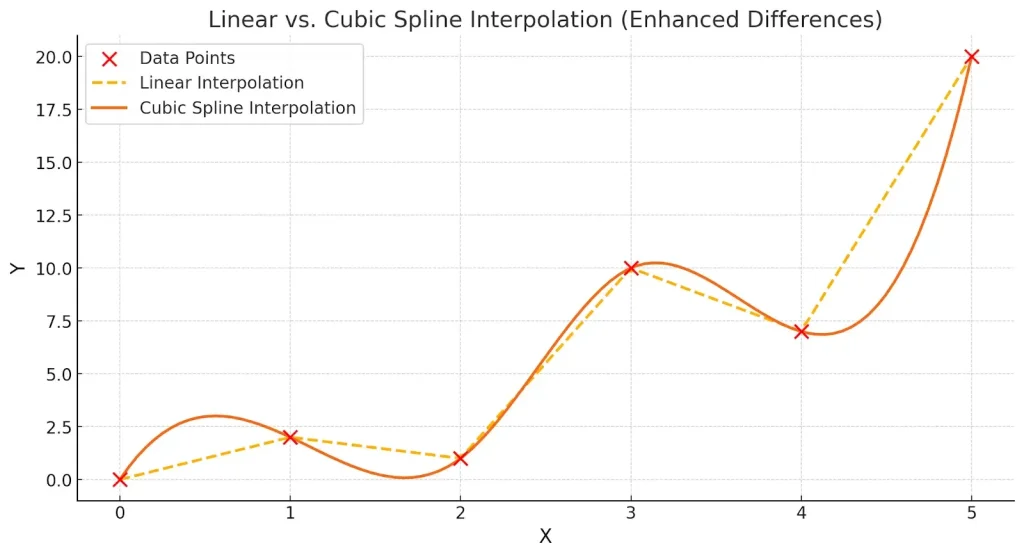
On the graph, you can see the difference between linear and spline interpolation. Spline interpolation smoothly joins each point with a curve, whereas linear interpolation has sharp edges at data points.
It is best suited where simplicity and speed are important and when the dataset is small.
Linear vs Polynomial Interpolation:
Polynomial interpolation uses a single polynomial that passes through the given points, Polynomial interpolation considers more than two points when interpolating as opposed to linear interpolation. Polynomial interpolation does provide a smooth curve but can suffer from unwanted oscillations for large data, thus it can be unreliable in some cases.
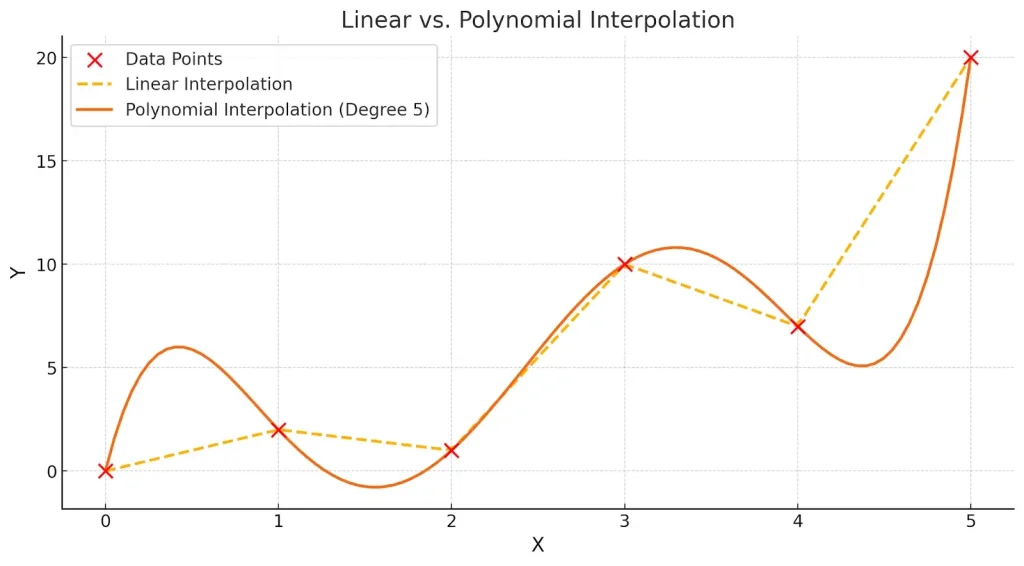
From the graph, we can see that it sacrifices smoothness and accuracy but is a simpler interpolation.
Tools for Performing Linear Interpolation:
You can perform manual calculations for simple and small datasets; for more complex and larger datasets, you may use Excel to automate the process with its built-in formulas. Another option is to use programming languages such as Python or MATLAB, but this requires familiarity with the aforementioned languages.
If all this seems too much hassle, you can alternatively utilise our user-friendly interpolation tool for quick results with the click of a button.