Online Interpolation Calculator for Accurate Data Estimation & Analysis
Linear Interpolation Calculator
Enter five known values and leave one empty.
Our free online Interpolation Calculator allows you to quickly and accurately estimate unknown values in your dataset, whether you’re working with simple linear or complex polynomial interpolation.
Nowadays, data analysis often requires identifying unknown values in a dataset. To determine an unknown value at a certain point, we use a method called interpolation. You can determine any missing value by using our Interpolation Calculator.
How to Use the Linear Interpolation Calculator- An Easy Step-by-Step Guide
Linear Interpolation is a mathematical technique for estimating unknown data within a known data set. Our online linear interpolation calculator simplifies the process and eliminates the hassle of manual calculations. Our step-by-step guide will help you become familiar with our calculator.
Features of the Linear Interpolation Calculator:
Simple and User-Friendly Interface: The interface is designed to be beginner-friendly, featuring highlighted areas for inputting values.
Instantaneous Results: Once you have typed the values in the calculator, just press the calculate button and the interpolated value will be calculated and displayed instantly.
Graphical Representation: Our tool also generates a graph for the values to help you visualize the data, allowing for an easy understanding of the data.
Responsive Design: Our tool works on all kinds of platforms, from desktops to mobile to tablets, you can enjoy this tool on any device you like
How to Use the Linear Interpolation Calculator?
Step 1: Enter the Known Values
Let’s use an example,
If you know 2 data points (A and B) in a dataset and want to interpolate for an unknown value at C.
A = X1, Y1 = (10,50)
B = X2, Y2 = (20,100)
C = X3, Y3 = (15,?)
Thus:
X1 = 10 Y1 = 50
X2 = 20 Y2 = 100
X3 = 15 Y3 = Unknown
Put these values in each box of the calculator.
Now press the calculate button.
The interpolated result for Y3 will be shown, alongside the equation of the interpolated line.
You can also see a visual representation of the interpolated points on the graph below.
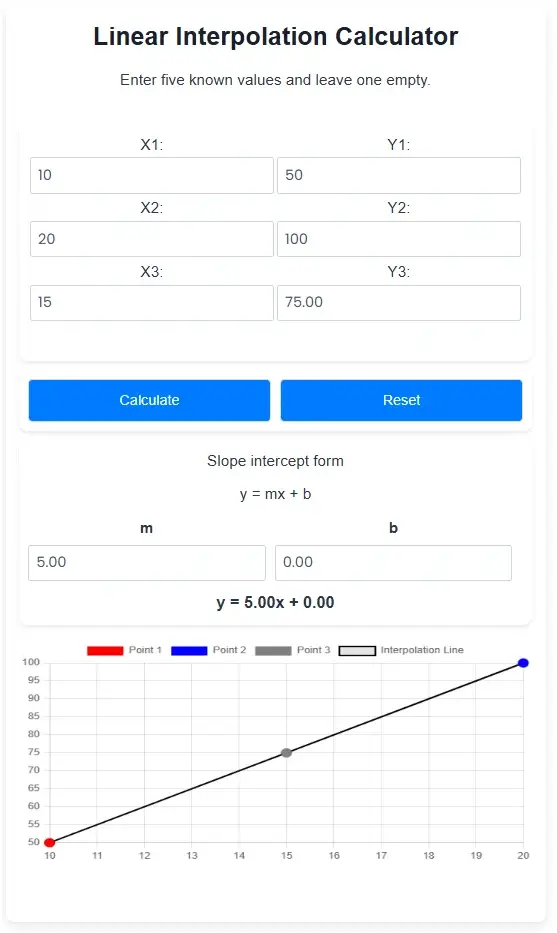
As you can see, the calculator is very easy to use, if you now want to interpolate another point, just press the reset button and you can put your new values in the calculator again.
How to Linear Interpolation Calculator Works:
In order to see how the tool is operating, we can see the basic linear interpolation formula that this calculator uses.
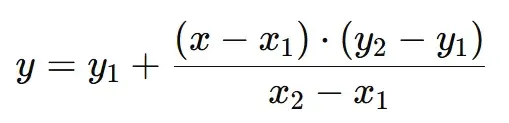
Where:
Y is the interpolated value for the given x
(x1,y1) and (x2,y2) are the two known points.
X is the point where you want to estimate the value of y
Let’s solve the above example using the Linear Interpolation Equation.
Given points:
A = (10,50)
B = (20,100)
C = (15,?)
Putting the above values in the equation:
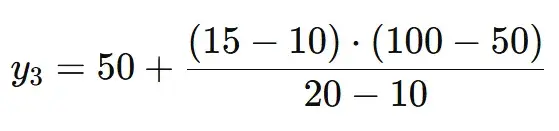
Solving to get the estimated y-value at point C which comes out to y3 =75.
Things to Look Out For:
This is the overall guide for using the linear interpolation calculator. If you need any further assistance, please use our Contact Us page.
What Is Interpolation and Why Is It Important for Data Analysis?
Interpolation is a mathematical method used to estimate any unknown value within a range of discrete known data points. We will go over the different types of interpolation techniques below but to understand it simply, imagine a farmer who measures a fruit tree’s height.
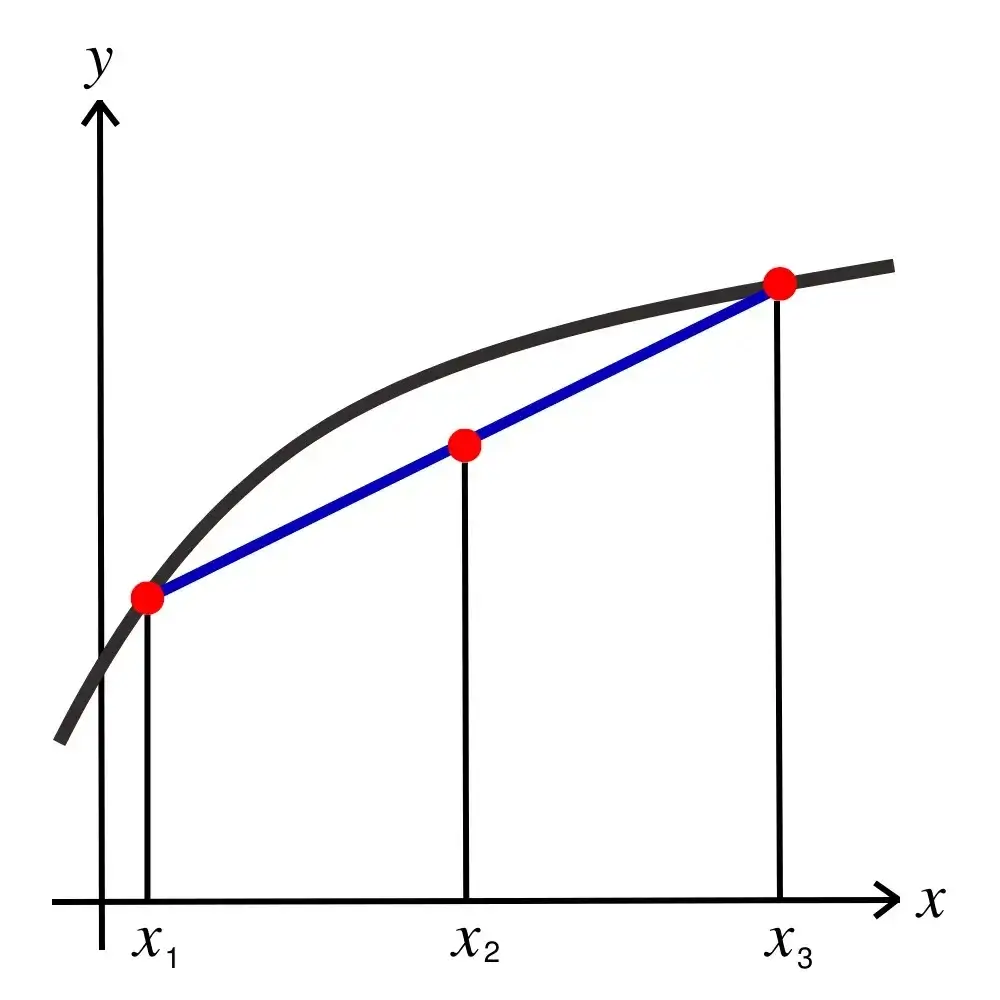
After 2 years of planting, the farmers see that the tree has grown 2 meters, then after another 2 years i.e. 4 years after planting, the tree has grown 4 meters. Here if the farmer wants to know the tree’s height at age 3, then by using an interpolation technique called Linear Interpolation, he can calculate it to be 3 meters.
Linear interpolation is one of the many different types of techniques used in the mathematical world. We will discuss some of the commonly used types in the article below.
Difference between Interpolation and Extrapolation:
Both interpolation and extrapolation are used to estimate values based on existing data. There is a subtle difference between the two, they are as follows:
Interpolation: Interpolation is used to find a value within a range of known data points. The tree that we previously discussed was an example of interpolation.
Extrapolation: Extrapolation is used to estimate the values outside of a data point. Using the previous example, if the farmer now wants to know what the height of the tree will be after 6 years while learning the height of the tree at 2 and 4 years, he can use extrapolation to find out the height.
Finding a value within a range of data is more accurate than finding a value of data outside of a known data point. Hence, Interpolation is generally more reliable because there is less uncertainty.
Real-Life Applications of Interpolation Across Various Fields
Interpolation is crucial in domains where data is in discrete form and needs to be processed. Some of them are:
Machine Learning:
Interpolation is commonly used in machine learning to create multiple data points from a known set of values, this is useful for improving model training and prediction.
Computer Graphics and Image Processing:
Interpolation is used to resize images to increase or decrease image resolution. It is used in 3D graphics and motion tracking to create smooth animations.
Environmental Sciences:
Weather prediction is mostly made using spatial interpolation by which temperature and humidity are measured in areas where direct measurement cannot be taken. Interpolation also creates a topographical mapping of the earth’s elevation at different points.
Different Types of Interpolation Methods
There are multiple types of interpolation techniques used for varying applications.
Linear Interpolation:
This method works by connecting two known data points with a straight line and estimating the unknown values between these points to be on this straight line. This is perfect for datasets where the rate of change is constant, and it gives accurate results for these kinds of data. An example of linear interpolation is a car travelling at a constant speed throughout a journey.
Polynomial Interpolation:
As the name suggests, this method uses polynomials of higher degrees to find unknown data.
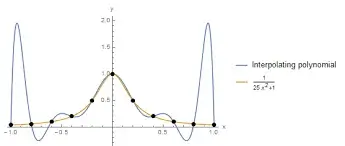
This is suitable for data which shows a non-linear trend. Now imagine a car accelerating from a stoplight, in this instance, the speed is changing and distance is in a non-linear relationship with time, here polynomial interpolation will be better suited to calculate the speed at any given time.
Spline Interpolation:
In spline interpolation, the data points are connected by a series of low-degree polynomials instead of a linear or a polynomial curve.
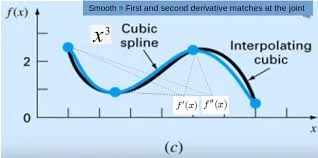
This interpolation technique provides a smooth and stable curve and is better suited for large data sets, making it more efficient than higher-degree polynomial interpolation.
Nearest Neighbour Interpolation:
This type of interpolation is the simplest and fastest compared to other methods, which makes
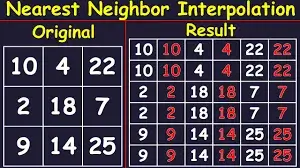
it suitable for real-time applications and scenarios with limited processing power, it assigns the value of the nearest known data point to the unknown point. This method is suitable for discrete data sets.
Logarithmic Interpolation:
Logarithmic Interpolation is a specialized type of interpolation used for specific data sets which follow a logarithmic trend, meaning that the data changes logarithmically and not linearly.
Newton Interpolation:
Newton Interpolation is a method of constructing an interpolation polynomial that passes through a given set of data. Its basic concept is of divided differences and it uses a recursive approach to calculate the polynomial’s coefficients efficiently. This method yields more stable results for unevenly spaced data points and has high accuracy for small to medium data sets.
Lagrange Interpolation
Lagrange interpolation is a numerical method which is used to approximate a function that passes through a given set of points. The difference is that, unlike linear interpolation, it fits a polynomial of degree n-1, where n is the number of data points. This feature makes it better suited for complex datasets.
Try our calculator now to see how different interpolation methods can solve your data analysis needs! You know we can also perform linear interpolation in excel as well.
Why Choose Our Interpolation Calculator:
The User Interface is simple to understand and use, which means that you will make fewer errors when inputting the values. You can choose from linear, polynomial, spline, and various other methods of interpolation which are available with just a click of a button.
Common Mistakes in Interpolation and How to Avoid Them
Choosing a wrong interpolation method can lead to inaccurate results, Multiple factors need to be accessed before deciding on the type of interpolation to be used, the most important factors to consider are:
Overfitting with High-Degree Polynomials:
Using a higher degree polynomial can cause inaccuracies in the results and can lead to oscillations. In this case, you can opt for spline interpolation or use a lower-degree polynomial interpolation method.
Data Patterns:
While interpolating values, it is important to look out for trends and anomalies in the known data, as anomalous values if used for interpolation can give vastly different and inaccurate results which does not align with the expected trend.
Not Validating Results:
It is important to check the final interpolated values and cross-check them with the given trend of the data, this will help you validate the results.
Assuming Incorrect data trend:
Given data can show different types of relationships, it is important to analyze the values first. Another issue is assuming the data to have a linear relationship when the actual data does not vary linearly. This will result in a huge error in the final result.
Using Incorrect units:
Using incorrect units can cause interpolation errors and thus it is important to convert all the values to the same unit to avoid errors. Before interpolating, always check the range of your known data points to ensure they’re not too far apart. If your data has significant outliers, consider using robust interpolation methods like spline interpolation instead of high-degree polynomials.
Manual Interpolation vs Using Our Calculator (Pros and Cons)
There are many advantages to using our interpolater. You can see the table below comparing manual interpolation vs using our online calculator.
| Aspect | Manual Interpolation | Our Calculator |
| Speed | Time-Consuming | Quick Results |
| Accuracy | May contain Human Error | High Precision |
| Learning Curve | Need to understand interpolation formulas | Easy-to-use Interface |
| Effort Required | Manual computation required | Results in one click. |
How to Easily Use the Linear Interpolation Calculator
The procedure to use the linear interpolation calculator is simple:
Step 1: Enter the known coordinates and the point on which to perform interpolation.
Step 2: Now click on the Calculate Button.
Step 3: The Interpolated point will be displayed below.
Conclusion
To sum up, interpolation helps you estimate missing values in data. Our Interpolation Calculator makes it easy to do this with methods like linear and polynomial interpolation. The tool is quick, accurate, and simple to use, making it perfect for anyone working with data.
Try our free calculator today and see how easy it is to calculate missing values. Whether you’re working with machine learning or data analysis, our tool can help you get accurate results fast. Start using it now and make your data analysis easier.